Практическая работа к главе 3

1. Представьте в электронной таблице свои расходы за неделю; для заполнения диапазонов ячеек B7:I7, I3:I7 используйте формулы. Образец структуры и оформления таблицы:

Скачав электронную таблицу, поменяйте данные в днях недели (например поменяйте цену проезда, так как могут разниться). Также можно добавить расходы, а формулы уже посчитают сколько в общем средств вы потратили. Скачать таблицу с выполненным заданием

2. Оформите лист для получения количества информации в разных единицах: Узнайте ёмкость в байтах жёсткого диска имеющегося в вашем распоряжении компьютера, запишите её в ячейку B2. Получите в ячейках B1, B3:B5 ёмкость жёсткого диска в единицах измерения, указанных в соответствующих ячейках столбца А.

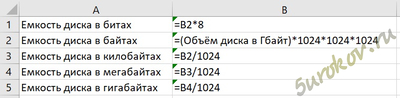
Заходим в "Мой компьютер" и узнаем объём своего жесткого диска. Так как там указано значение в гигабайтах, а нам необходимо поместить значение в байтах в ячейку B2, переведем из гигабайт в байт. Мой пример: 465 Гбайт = 465*1024*1024*1024 байт. Это значение я и поместил в ячейку в виде формулы (=465*1024*1024*1024). Далее уже можете увидеть на изображении или скачать файл таблицы, подставив своё значение.
Скачать таблицу с выполненным заданием

3. Составьте таблицу умножения на число n (1 <= n <= 9). Значение n задаётся в ячейке B2.

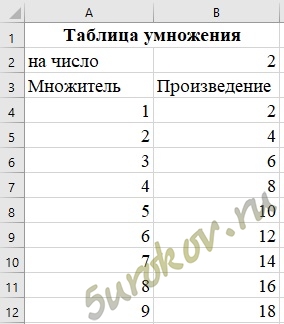
Скачать таблицу с выполненным заданием

4. Составьте таблицу умножения чисел первого десятка. Используйте смешанные ссылки.

Скачать таблицу с выполненным заданием

5. Подготовьте таблицу.
Значения в диапазоне ячеек B1:B20 получите автозаполнением. Выполните следующие расчёты:
а) получите сумму всех целых чисел от 1 до 20 в ячейке B21;
б) получите в диапазоне ячеек C1:C20 квадраты соответствующих чисел из столбца В и сумму квадратов в ячейке С21;
в) получите в диапазоне ячеек D1:D20 первые 20 чётных чисел и их сумму в ячейке D21.

Скачать таблицу

7. Как известно, игра в шахматы была придумана в Индии. Согласно старинной легенде, индусский царь, восхищённый игрой, решил щедро одарить её изобретателя. Но тот, по мнению царя, запросил ничтожную награду: он просил выдать одно пшеничное зерно за первую клетку шахматной доски, а за каждую следующую клетку (всего их 64) — вдвое больше против предыдущей. Рассчитайте, сколько всего пшеничных зёрен должен был получить изобретатель. Какими могли бы быть размеры амбара для размещения этого зерна, если кубический метр пшеницы содержит около 15 миллионов зёрен?

Всего зёрен у нас получилось 9223372036854780000 штук. Разделим на 15 миллионов мы получаем размеры амбара, получилось 614891469124 (м³)
Скачать таблицу с выполненным заданием

8. Известно количество учеников во всех классах начальной школы: Определите, насколько число учеников в самом многочисленном классе превышает число учеников в самом малочисленном классе. Вычислите среднюю наполняемость классов.

Скачать таблицу с выполненным заданием

9. Постройте таблицу истинности для логического выражения НЕ (А ИЛИ В).

Скачать таблицу с выполненным заданием

10. Известно количество учеников во всех классах начальной школы. Класс, в котором более 25 учеников, считается переполненным. Используя данные практического задания 8, создайте таблицу следующего вида:
В столбце С дайте комментарии («переполнен», «соответствует норме») по наполняемости каждого класса. Подсчитайте, сколько классов переполнено и сколько имеет наполняемость, соответствующую норме.

Скачать таблицу с выполненным заданием

11. С помощью Мастера диаграмм постройте столбчатую и круговую диаграммы своих расходов за неделю. Воспользуйтесь таблицей, полученной при выполнении практического задания 1.
Столбчатая диаграмма «Расходы по статьям* строится по данным несмежных диапазонов ячеек A3:A6, I3:I6. Круговая диаграмма «Расходы по дням недели* строится по данным несмежных диапазонов ячеек B2:H2, B7:H7.

Скачать таблицу с выполненным заданием

12. С помощью Мастера диаграмм (тип диаграммы — Точечная) постройте графики следующих функций:
а) у = |х| для значений аргумента, изменяющихся от -10 до 10 с шагом 1;
б) у = 2х²+ 5х - 10 для значений аргумента, изменяющихся от -5 до 2,5 с шагом 0,5;
в) у = х² - 2|х| - 3 для значений аргумента, изменяющихся от -3,5 до 3,5 с шагом 0,5.

Скачать таблицу с выполненным заданием

<- Параграф 3.3 Наверх Тестовые задания к главе 3 ->