Составьте алгоритм для решения задачи, аналогичной предыдущей, с учетом того, что точки расположены в трехмерном пространстве

Составьте алгоритм для решения задачи, аналогичной предыдущей, с учетом того, что точки расположены в трехмерном пространстве.

Формула нахождения длины отрезка по двум точкам:

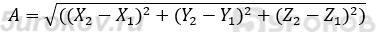
Алгоритм с полным перебором:
NumberX1:=1;
NumberY1:=1;
NumberZ1:=1;
NumberX2:=1;
NubmerY2:=2;
NubmerZ2:=1;
for i:=1 to N do
   for j:=1 to N do
      if sqrt(sqr(X[i] – X[j]) + sqr(Y[i]-Y[j]) + sqr(Z[i]-Z[j])) > sqrt(sqr(NumberX2-NumberX1) + sqr(NubmerY2-NubmerY1) + sqr(NubmerZ2-NubmerZ1))
   then
   begin
NumberX1:= X[i];
NumberY1:= Y[i];
NumberZ1:= Z[i];
NumberX2:= X[j];
NubmerY2:= Y[j];
NubmerZ2:= Y[j];
end;

Алгоритм с неполным перебором:
NumberX1:=1;
NumberY1:=1;
NumberZ1:=1;
NumberX2:=1;
NubmerY2:=2;
NubmerZ2:=1;
for i:=1 to N do
   for j:=i+1 to N do
      if sqrt(sqr(X[i] – X[j]) + sqr(Y[i]-Y[j]) + sqr(Z[i]-Z[j])) > sqrt(sqr(NumberX2-NumberX1) + sqr(NubmerY2-NubmerY1) + sqr(NubmerZ2-NubmerZ1))
      then
      begin
NumberX1:= X[i];
NumberY1:= Y[i];
NumberZ1:= Z[i];
NumberX2:= X[j];
NubmerY2:= Y[j];
NubmerZ2:= Y[j];
end;