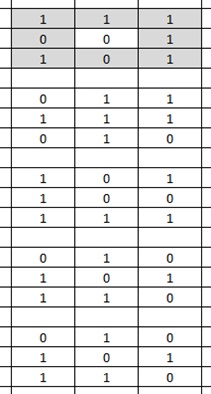
Ответы по параграфу 26 Пример имитационной модели

Задание 1. Где используется метод имитационного моделирования?

Метод имитационного моделирования может использоваться:
1. Бизнес-процессы
2. Боевые действия
3. Динамика населения
4. Дорожное движение
5. Железнодорожные перевозки
6. ИТ-инфраструктура
7. Логистика
8. Математическое моделирование исторических процессов
9. Пешеходная динамика
10. Производство
11. Рынок и конкуренция

Задание 2. В чем отличие эволюционной задачи, решавшейся методом математического моделирования в § 25, от задачи, решавшейся в данном параграфе методом имитационного моделирования?

В математическом моделировании мы проследили, как за 10 лет будет меняться число карпов в зависимости от количества выпущенных рыб. В имитационном моделированим мы проследили изменения в расселении живых организмов со сменой поколений.

Задание 3. Проведите вычислительный эксперимент на линейной имитационной модели для различных вариантов исходного расселения организмов, отвечающий на следующие вопросы.

а) Возможно ли такое расселение, при котором все организмы в конце концов вымрут?
Нет, невозможно. Если даже в одной только ячейке будет жизнь, в следующем поколении уже будет 5 ячеек живых.

б) Не ведет ли любое расселение в конечном итоге к одной и той же последовательности поколений?
Да, ведёт. Вот некоторые примеры расселений:

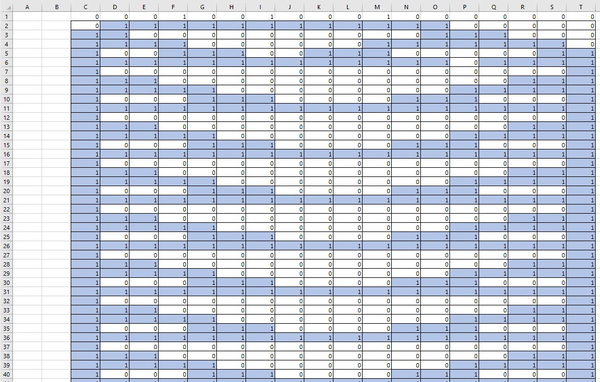
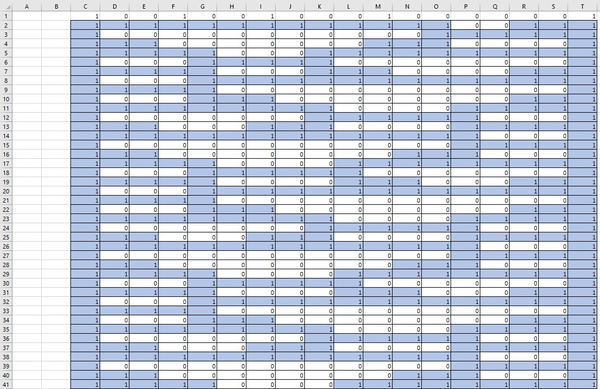
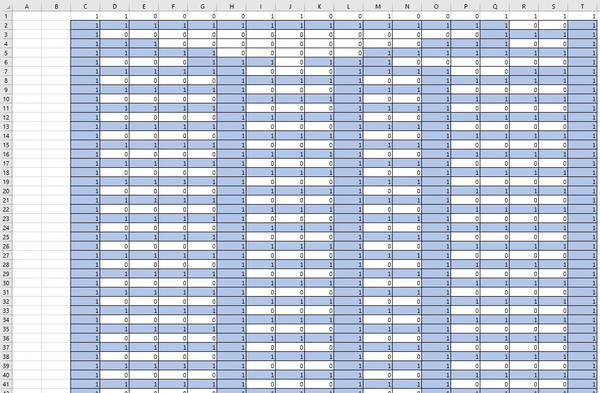
в) Что меняется с изменением размера жизненного пространства?
С уменьшением жизненного пространства во втором поколении увеличивается количество жизни в новом пространстве.

Задание 4. Постройте в электронных таблицах двумерную модель «Жизнь». Проведите вычислительный эксперимент с разными вариантами первоначального расселения организмов. Попробуйте найти такие первоначальные расселения, которые:

Скачать электронную таблицу
Формула: =ЕСЛИ(ИЛИ(И(C2=1;СУММ(B1:D3)>=3;СУММ(B1:D3)<=4); И(C2=0; СУММ(B1:D3)=3)); 1; 0)

В нашем условии должно выполнятся одно из двух условий, чтобы ячейка жила:
1) И(C2=1;СУММ(B1:D3)>=3;СУММ(B1:D3)<=4) в данном случае ячейка должна быть жива (C2=1), а соседей должно быть меньше или равно трём (СУММ(B1:D3)<=4) и должно быть больше двух или равно двум (СУММ(B1:D3)>=3). Так как у нас клетка живая, то в неравенства прибавляем единицу.
2) И(C2=0; СУММ(B1:D3)=3) в этом случае клетка должна быть мертвая. Чтобы в следующем поколении зародилась жизнь, у нее должно быть ровно три живых соседа.

а) обречены на гибель

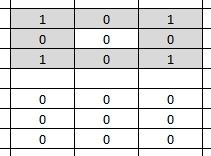
б) не меняются со сменой поколений

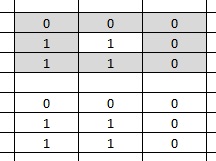
в) ведут к периодической смене повторяющихся конфигураций расселения