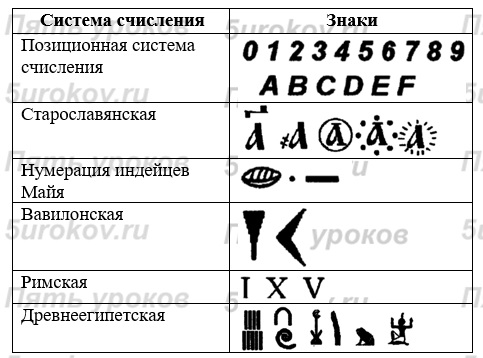
Ответы по параграфу 1.1 Системы счисления
12-ричная система счисления появилась после 10-тичной из-за её удобства. 12 – это количество фалангов на 4-ёх пальцах – указательном, среднем, безымянном и мизинце. Большой не считаем, так как у него третий фаланг скрыт в ладони. Также 12 является делителем 3 и 4.
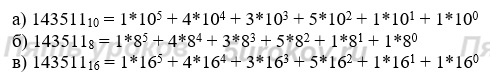
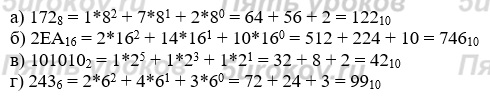
1100112 = 5110
1114 = 2110
358 = 2910
1B16 = 2710
а) Наибольшее: 1100112
б) Наименьшее: 1114
2225 = 6210
1115 = 3110
2415 = 7110

Ответ: равенство под а) верно, а под б) неверно, значения не равны друг другу.

б) 60010 = 10010110002

в) 202010 = 111111001002

Старый учебник:
201010 = 111110110102
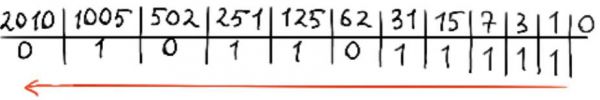
б) 60010 = 11308
в) 202010 = 37448
б) 60010 = 25816
в) 202010 = 7E416
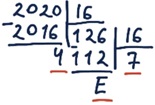
б) 1010 + 1010 = 10100
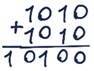
в) 10101 + 111 = 11100
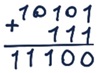
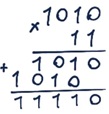
б) 111*101 = 100011
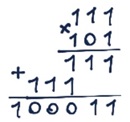
в) 1010*111 = 1000110
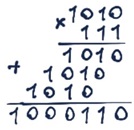
б) 10101 – 1101 = 1000
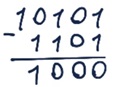
в) 10101 – 1111 = 110
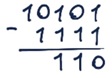
б) 1100 : 10 – 10 = 100 (12 : 2 – 2 = 4);
в) 1100 : 11 – 100 = 0 (12 : 3 – 4 = 0).

• двоичные числа в компьютере представлены с помощью простых технических элементов с двумя устойчивыми состояниями;
• надёжность и помехоустойчивость;
• двоичная арифметика наиболее проста.
Недостатки:
• большая длина кода при обмене информацией между компьютерами:
• зрительная однородность, из-за одних нулей и единиц человеку сложно разобраться в коде.
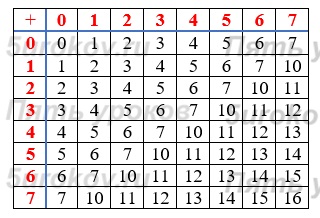
Таблица умножения в восьмеричной системе счисления
 Решение заданий из учебника Информатика 8 класс Босова, параграф 1.1 Системы счисления. Общие сведения о системах счисления, двоичная система счисления, Восьмеричная и шестнадцатеричная система счисления, двоичная арифметика
Решение заданий из учебника Информатика 8 класс Босова, параграф 1.1 Системы счисления. Общие сведения о системах счисления, двоичная система счисления, Восьмеричная и шестнадцатеричная система счисления, двоичная арифметика
Задание 3. Цифры каких систем счисления приведены на рисунке 1.1?

Задание 4. Объясните, почему позиционные системы счисления с основаниями 5, 10, 12 и 20 называют системами счисления анатомического происхождения.
Сначала люди считали всё на пальцах и это было удобно. Система счисления с основанием 5 – это число пальцев на одной руке. После стало не хватать пальцев на одной руке и начали использовать обе руки. Так появилась 10-ричная система счисления. 20-ричная система появилась, когда не хватало пальцев на руках и стали использовать пальцы ног.12-ричная система счисления появилась после 10-тичной из-за её удобства. 12 – это количество фалангов на 4-ёх пальцах – указательном, среднем, безымянном и мизинце. Большой не считаем, так как у него третий фаланг скрыт в ладони. Также 12 является делителем 3 и 4.
Задание 5. Как от свёрнутой формы записи десятичного числа перейти к его развёрнутой форме?
Необходимо умножить цифры числа на «веса» разрядов и сложить полученные произведения.Задание 6. Запишите в развёрнутой форме числа:
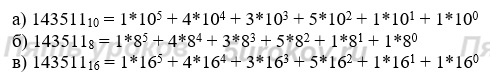
Задание 7. Вычислите десятичные эквиваленты следующих чисел:
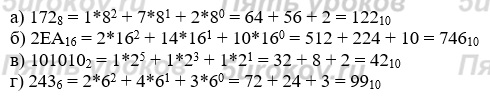
Задание 8. Укажите, какое из чисел 1100112, 1114, 358 и 1B16 является:
Переведём все числа в десятичную систему счисления:1100112 = 5110
1114 = 2110
358 = 2910
1B16 = 2710
а) Наибольшее: 1100112
б) Наименьшее: 1114
Задание 9. Какое минимальное основание имеет система счисления, если в ней записаны числа 123, 222, 111, 241? Определите их десятичный эквивалент.
Минимальное основание – 5. Это пятеричная система счисления, так как в записи у одного из чисел присутствует цифра 4. 1235 = 1*25 + 2*5 + 3*1 = 38102225 = 6210
1115 = 3110
2415 = 7110
Задание 10. Верны ли следующие равенства?
Чтобы проверить равенства, переведём числа в десятичную систему счисления.
Ответ: равенство под а) верно, а под б) неверно, значения не равны друг другу.
Задание 11. Найдите основание x системы счисления, если:
Запишем развернутую форму числа с неизвестным основанием и приравняем его ко второму.
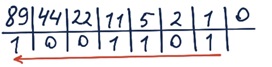
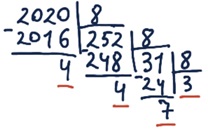
Задание 12. Переведите целые числа из десятичной системы счисления в двоичную.
а) 8910 = 10110012
б) 60010 = 10010110002

в) 202010 = 111111001002

Старый учебник:
201010 = 111110110102
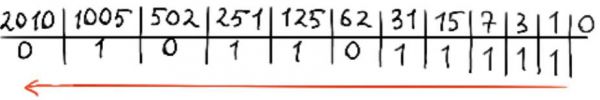
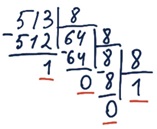
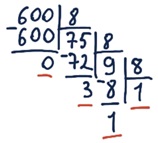
Задание 13. Переведите целые числа из десятичной системы счисления в восьмеричную.
а) 51310 = 10018
б) 60010 = 11308

в) 202010 = 37448

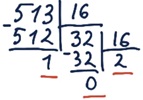
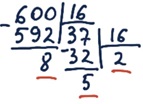
Задание 14. Переведите целые числа из десятичной системы счисления в шестнадцатеричную.
а) 51310 = 20116
б) 60010 = 25816

в) 202010 = 7E416
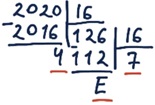
Задание 15. Заполните таблицу.
| Основание 2 | Основание 8 | Основание 10 | Основание 16 |
|---|---|---|---|
| 101010 | 52 | 42 | 2A |
| 1010111 | 127 | 87 | 57 |
| 101000001 | 501 | 321 | 141 |
| 101010 | 52 | 42 | 2A |
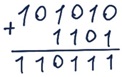
Задание 16. Выполните операцию сложения над двоичными числами:
а) 101010 + 1101 = 110111
б) 1010 + 1010 = 10100
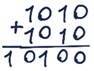
в) 10101 + 111 = 11100
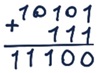
Задание 17. Выполните операцию умножения над двоичными числами:
а) 1010*11 = 11110
б) 111*101 = 100011
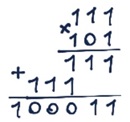
в) 1010*111 = 1000110
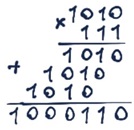
Задание 18. Выполните операцию вычитания:
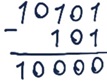
а) 10101 – 101 = 10000
б) 10101 – 1101 = 1000
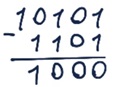
в) 10101 – 1111 = 110
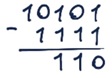
Задание 19. Расставьте знаки арифметических операций, чтобы были верны следующие равенства в двоичной системе.
Задание выполняется проще, если представить операнды и результат в десятичной системе счисления. а) 1100 * 11 – 100 = 100000 (12 * 3 – 4 = 32);б) 1100 : 10 – 10 = 100 (12 : 2 – 2 = 4);
в) 1100 : 11 – 100 = 0 (12 : 3 – 4 = 0).
Задание 20. Вычислите выражения:

Задание 21. Какими преимуществами и недостатками обладает двоичная система счисления по сравнению с десятичной?
Преимущества:• двоичные числа в компьютере представлены с помощью простых технических элементов с двумя устойчивыми состояниями;
• надёжность и помехоустойчивость;
• двоичная арифметика наиболее проста.
Недостатки:
• большая длина кода при обмене информацией между компьютерами:
• зрительная однородность, из-за одних нулей и единиц человеку сложно разобраться в коде.
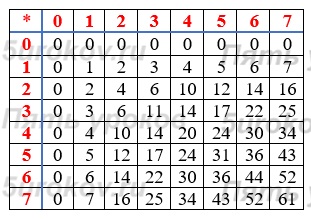
Задание 22. Разработайте таблицы сложения и умножения для восьмеричной системы счисления.
Таблица сложения в восьмеричной системе счисления
Таблица умножения в восьмеричной системе счисления

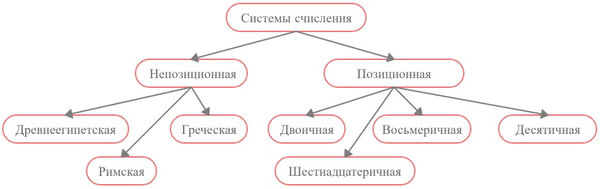
Задание 23. Постройте граф, отражающий разновидности систем счисления.
 Решение заданий из учебника Информатика 8 класс Босова, параграф 1.1 Системы счисления. Общие сведения о системах счисления, двоичная система счисления, Восьмеричная и шестнадцатеричная система счисления, двоичная арифметика
Решение заданий из учебника Информатика 8 класс Босова, параграф 1.1 Системы счисления. Общие сведения о системах счисления, двоичная система счисления, Восьмеричная и шестнадцатеричная система счисления, двоичная арифметика
