Ответы по параграфу 1.3 Элементы теории множеств и комбинаторики
Немного теории по теме «Элементы теории множеств и комбинаторики»:
Пересечением (обозначается ⋂) двух множеств называется множество их общих элементов.
Например: A = {1, 2, 3}; B = {2, 5, 7}; A ⋂ B = {2}
Объединение (обозначается ∪) двух множеств называется множество, состоящее из всех элементов этих множеств и не содержащее никаких других элементов.
Например: A = {1, 2, 3}; B = {2, 5, 7}; A ∪ B = {1, 2, 3, 5, 7}
Задание 2. Задайте путем перечисления всех элементов:
а) О = {0, 1, 2, 3, 4, 5, 6, 7}
б) К = {000, 001, 010, 011, 100, 101, 110, 111}
Задание 3. Пусть М = {а, б, в}, Р = {а, б, г, д, и}, К = {г, д, и}. Обсудите в группе и запишите с помощью фигурных скобок или знака ∅:
а) M ⋂ P = {а, б}
б) M ⋂ K = ∅
в) K ⋂ P = {г, д, и}
г) M ∪ P = {а, б, в, г, д, и}
д) M ∪ K = {а, б, в, г, д, и}
е) K ∪ P = {а, б, г, д, и}
ж) дополнение К до Р = {а, б}
з) дополнение ∅ до М = {а, б, в}
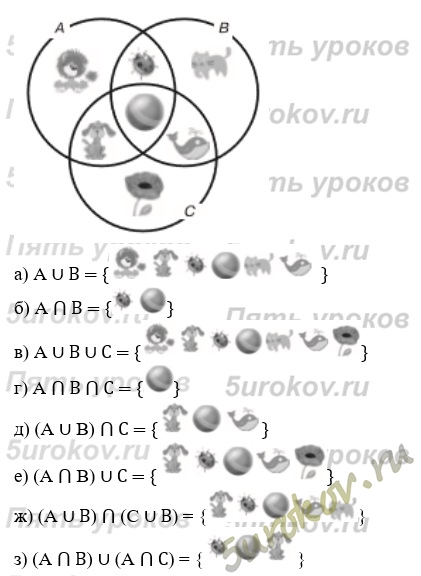
Задание 5. Из каких элементов состоит:
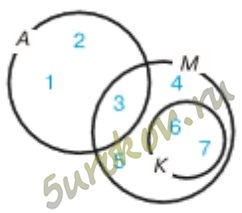
а) K ∪ M = {3, 4, 5, 6, 7}
б) K ⋂ M = {6, 7}
в) дополнение К до М = {3, 4, 5}
г) дополнение (M ⋂ A = {3}) до М = {4, 5, 6, 7}
2) (20 + 11) – 25 = 6 учеников занимаются и математикой и биологией.
Задание 7. Для составления цепочек используются бусины, помеченные буквами: M, N, O, P, S. Сколько разных цепочек можно составить из трех бусин, для которых выполняются следующие условия:
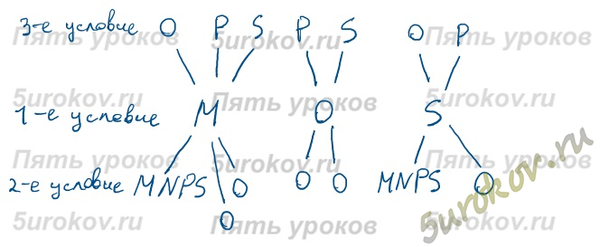
Ответ: 13 различных цепочек.
По середине у нас бусины M, O, S (1-е условие), по 3-му условию на первом месте у нас бусины O, P, S, не стоящие в цепочке в середине.
Для М на первом месте могут быть O, P, S. Для O на первом месте могут быть P, S (O не может быть на первом месте, так как в середине уже стоит такая бусина). Для S на первом месте могут быть O, P.
Чтобы выбрать третью бусину, мы придерживаемся 2-му условию. Так у нас получится 13 вариантов цепочек.

Ответ: 16 способов
Перечислим оставшиеся варианты:
АААР;
ААРА;
ААРР;
АРАА;
АРАР;
АРРА;
АРРР;
РААА;
РААР;
РАРА;
РАРР;
РРАА;
РРАР;
РРРА.

Графический ключ:
Выбор первого элемента можно осуществить пятью способами. Второго – четырьмя способами. Третьего – тремя способами. Четвертого – двумя способами. Пятого элемента – одним. Посчитаем всевозможные перестановки по правилу произведения и получаем:
5*4*3*2*1=120 различных комбинаций у графического ключа, разработанным Иваном.
Трехзначный цифровой пароль:
Длина пароля равна k = 3. Если считать, что нами используются стандартная цифровая клавиатура, а в нем 10 цифр (0, 1, 2, ..., 9), тогда у нас N = 10.
Максимальное количество комбинаций: M=Nk=103=1000
Комбинаций в трехзначном цифровом пароле, вводимого со стандартной цифровой клавиатуры намного больше, чем при использовании графического ключа в виде пятиугольника. То есть Иван не прав.
Ответ: Иван не прав.
Так как все нули, то подмножество будет пустым.
01110 – {3, 5, 7}
Так как на 2, 3, 4 местах присутствует 1, то подмножество будет {3, 5, 7}
00111 – {5, 7, 9}
Так как на 3, 4 и 5 местах присутствует 1, то подмножество будет {5, 7, 9}
11111 – {1, 3, 5, 7, 9}
Так как везде присутствует 1, то подмножество будет {1, 3, 5, 7, 9}
Можно сказать, что у множества М может быть 32 различных подмножеств. Решение заданий из учебника Информатика 8 класс Босова, параграф 1.3 Элементы теории множеств и комбинаторики. Множество, операции над множествами, правила суммы и произведения.
Немного теории по теме «Элементы теории множеств и комбинаторики»:
Пересечением (обозначается ⋂) двух множеств называется множество их общих элементов.
Например: A = {1, 2, 3}; B = {2, 5, 7}; A ⋂ B = {2}
Объединение (обозначается ∪) двух множеств называется множество, состоящее из всех элементов этих множеств и не содержащее никаких других элементов.
Например: A = {1, 2, 3}; B = {2, 5, 7}; A ∪ B = {1, 2, 3, 5, 7}
Задание 2. Задайте путем перечисления всех элементов:
а) множество О всех цифр, используемых для записи чисел в восьмеричной системе счисления;
б) множество К всех цепочек из 0 и 1, состоящих ровно из трех символов.
а) О = {0, 1, 2, 3, 4, 5, 6, 7}б) К = {000, 001, 010, 011, 100, 101, 110, 111}
Задание 3. Пусть М = {а, б, в}, Р = {а, б, г, д, и}, К = {г, д, и}. Обсудите в группе и запишите с помощью фигурных скобок или знака ∅:
а) M ⋂ P = {а, б}б) M ⋂ K = ∅
в) K ⋂ P = {г, д, и}
г) M ∪ P = {а, б, в, г, д, и}
д) M ∪ K = {а, б, в, г, д, и}
е) K ∪ P = {а, б, г, д, и}
ж) дополнение К до Р = {а, б}
з) дополнение ∅ до М = {а, б, в}
Задание 4. Обсудите в группе и запишите с помощью фигурных скобок множества:

Задание 5. Из каких элементов состоит:
а) объединение К и М;
б) пересечение К и М;
в) дополнение К до М;
г) дополнение пересечения М и А до М?

а) K ∪ M = {3, 4, 5, 6, 7}
б) K ⋂ M = {6, 7}
в) дополнение К до М = {3, 4, 5}
г) дополнение (M ⋂ A = {3}) до М = {4, 5, 6, 7}
Задание 6. В классе 35 учеников. 20 – из них занимаются в математическом кружке, 11 – в биологическом, а 10 ничем не занимаются. Сколько ребят занимаются и математикой, и биологией?
1) Найдем тех ребят, которые посещают кружки, убрав из общего числа учеников тех, кто ничем не занимается: 35 – 10 = 25 учеников.2) (20 + 11) – 25 = 6 учеников занимаются и математикой и биологией.
Задание 7. Для составления цепочек используются бусины, помеченные буквами: M, N, O, P, S. Сколько разных цепочек можно составить из трех бусин, для которых выполняются следующие условия:
1) в середине цепочки стоит одна из бусин M, O, S;
2) третья бусина – любая гласная, если первая буква согласная, и любая согласная, если первая буква гласная;
3) на первом месте – одна из бусин O, P, S, не стоящая в цепочке в середине?

Ответ: 13 различных цепочек.
По середине у нас бусины M, O, S (1-е условие), по 3-му условию на первом месте у нас бусины O, P, S, не стоящие в цепочке в середине.
Для М на первом месте могут быть O, P, S. Для O на первом месте могут быть P, S (O не может быть на первом месте, так как в середине уже стоит такая бусина). Для S на первом месте могут быть O, P.
Чтобы выбрать третью бусину, мы придерживаемся 2-му условию. Так у нас получится 13 вариантов цепочек.
Задание 8. Сколько существует способов составить слово «ВИРУС», начиная с буквы В и двигаясь вправо или вниз до последней буквы?

Ответ: 16 способов
Задание 9. Алла Радугина защитила свой компьютер одним из четырехсимвольных паролей, составленных из букв «А» и «Р». Сколько всего существует вариантов таких паролей? Перечислите их.
Пароль у Аллы должен состоять из букв "А" и "Р", поэтому пароль не может быть "АААА" и "РРРР".Перечислим оставшиеся варианты:
АААР;
ААРА;
ААРР;
АРАА;
АРАР;
АРРА;
АРРР;
РААА;
РААР;
РАРА;
РАРР;
РРАА;
РРАР;
РРРА.
Задание 10. Каждый пользователь некой компьютерной системы получает уникальный идентификатор, представляющий собой k-символьную цепочку в четырехбуквенном алфавите. Укажите наименьшее k, позволяющее зарегистрировать в системе не менее тысячи пользователей.

Задание 11. Иван разработал приложение для планшета и защитил его оригинальным графическим ключом, использовав в качестве узлов вершины пятиугольника (каждую из вершин надо задействовать ровно один раз). Прав ли Иван, утверждая, что количество комбинаций его графического ключа ничуть не меньше, чем количество вариантов трехзначного цифрового пароля, вводимого со стандартной цифровой клавиатуры?
Посчитаем количество комбинаций в графическом ключе(в виде пятиугольника, вершину можно использовать один раз) и в трехзначном цифровом пароле.Графический ключ:
Выбор первого элемента можно осуществить пятью способами. Второго – четырьмя способами. Третьего – тремя способами. Четвертого – двумя способами. Пятого элемента – одним. Посчитаем всевозможные перестановки по правилу произведения и получаем:
5*4*3*2*1=120 различных комбинаций у графического ключа, разработанным Иваном.
Трехзначный цифровой пароль:
Длина пароля равна k = 3. Если считать, что нами используются стандартная цифровая клавиатура, а в нем 10 цифр (0, 1, 2, ..., 9), тогда у нас N = 10.
Максимальное количество комбинаций: M=Nk=103=1000
Комбинаций в трехзначном цифровом пароле, вводимого со стандартной цифровой клавиатуры намного больше, чем при использовании графического ключа в виде пятиугольника. То есть Иван не прав.
Ответ: Иван не прав.
Задание 12. Итак, в двоичном алфавите можно составить 25 различных 5-символьных слов или цепочек из пяти 0 и 1: 00000, 00001, …., 11110, 11111. Вернемся к нашему множеству М = {1, 3, 5, 7, 9}. Попробуем закодировать его подмножество полученными двоичными цепочками: если на первом месте в цепочке присутствует единица, то в соответствующее подмножество входит цифра 1; если единица присутствует на втором месте в цепочке, то в соответствующее подмножество входит цифра 3 и т.д. Запишите подмножества, соответствующие цепочкам 00000, 01110, 00111, 11111. Что вы можете теперь сказать о количестве подмножеств множества М?
00000 – ∅ пустое подмножествоТак как все нули, то подмножество будет пустым.
01110 – {3, 5, 7}
Так как на 2, 3, 4 местах присутствует 1, то подмножество будет {3, 5, 7}
00111 – {5, 7, 9}
Так как на 3, 4 и 5 местах присутствует 1, то подмножество будет {5, 7, 9}
11111 – {1, 3, 5, 7, 9}
Так как везде присутствует 1, то подмножество будет {1, 3, 5, 7, 9}
Можно сказать, что у множества М может быть 32 различных подмножеств. Решение заданий из учебника Информатика 8 класс Босова, параграф 1.3 Элементы теории множеств и комбинаторики. Множество, операции над множествами, правила суммы и произведения.
