Ответы по параграфу 2.4 Основные алгоритмические конструкции
Основные алгоритмические конструкции. Ветвление – Скачать презентацию
Основные алгоритмические конструкции. Повторение – Скачать презентацию
В линейном алгоритме не зависит последовательность выполняемых действий от исходных данных, так как алгоритм выполняет последовательный порядок действий без повторов.
Алгоритм как собраться в школу
1. Поставить будильник на 7 00 утра
2. Проснуться в 7 00
3. Выключить будильник
4. Пойти умываться
5. Позавтракать
6. Собрать учебники , тетради, пенал
7. Одеться
8. Взять вторую обувь
9. Выйти из дома.
б) из литературного произведения:
Алгоритм как разбудить ребенка из стихотворения
1. Лучик солнечный проснулся,
2. Улыбнулся,
3. потянулся
4. И пошёл будить сестричек —
Маленьких весёлых птичек.
5. Птички песенку запели,
6. И проснулся лес от трели.
7. Нежно глазки открывая,
Встала феечка лесная,
8. Разбудила медвежат,
И зайчаток, и мышат,
9. Полетела помогать
Всех девчонок поднимать.
10. Сядет фея на подушку,
11. «С добрым утром!» — шепнёт в ушко,
12. Поцелует нос и щёчки
Маминой любимой дочке,
13. Тихо скажет: «Динь-дилень!
Пусть хорошим будет день!»
в) из любой предметной области, изучаемой в школе:
Построение таблиц истинности для логических выражений
1. подсчитать n — число переменных в выражении;
2. подсчитать общее число логических операций в выражении;
3. установить последовательность выполнения логических операций с учётом скобок и приоритетов;
4. определить число столбцов в таблице: число переменных + число операций;
5. заполнить шапку таблицы, включив в неё переменные и операции в соответствии с последовательностью, установленной в п.3;
6. определить число строк в таблице (не считая шапки таблицы): m=2n;
7. выписать наборы входных переменных с учётом того, что они представляют собой целый ряд n-разрядных двоичных чисел от 0 до 2n - 1;
8. провести заполнение таблицы по столбцам, выполняя логические операции в соответствии с установленной последовательностью.
Задание 5. По алгоритму восстановите формулу.
Восстановите формулу вычисления у для произвольного значения X.
Ответ: у = ((2х + 3)х + 4)х + 5; у = 14 при х= 1.
Задание 9. Исходное данное — целое трёхзначное число х. Выполните для х = 125 следующий алгоритм.

Смысл результата – это сумма цифр числа х
Задание 10. Определите значение целочисленных переменных х и у после выполнения алгоритма.

Нет не согласен, при разветвляющимися алгоритме, в зависимости от результатов проверки условия, выполняется одна из двух последовательностей действий.
Подготовка домашнего задания
1. Определить список уроков на завтра по расписанию.
2. Если завтра есть математика или физика, то позаниматься с репетитором.
Если нет, перейти к п.4.
4. Определить, что задали по каждому уроку из расписания на завтра.
5. Выполнить домашнее задание по каждому уроку.
Или вот такой:
Погреть себе еды
1. Взять тарелку.
2. Если тарелка гразная, помыть ее.
3. Положить еду.
4. Поставить в микроволновку.
б) из литературного произведения:
Как обвенчаться
Ромео и Джульета влюбляются друг в друга.
Если их семьи враждуют, венчаться тайно. В противном случае играть пышную свадьбу.
в) из любой предметной области, изучаемой в школе.
Ответ: Данный алгоритм считает количество неотрицательных чисел среди двух чисел A и B.
Решение:
если chislo=3 то y:=’Понедельник’
если chislo=4 то y:=’Вторник’
если chislo=5 то y:=’Среда’
если chislo=6 то y:=’Четверг’
если chislo=0 то y:=’Пятница’
если chislo=1 то y:=’Суббота’
если chislo=2 то y:=’Воскресенье’
Сначала найдём понедельник 31-го января по формуле: chislo:=chislo mod 7, где chislo = 31.
31 mod 7 = 31/7 (ост) = 31 – 4*7 = 31-28 = 3
То есть, для chislo = 3 будет y='Понедельник'
Найдём для остальных дней января:
30 mod 7 = 2 – то есть будет воскресенье для chislo=2, так как предыдущий день. И так далее.
Нам нужно посчитать сначала 2 расстояния по координатам, и потом их сравнить. Ответом будет минимальное.
Алгоритм:
1. Определить координаты точки А.
2. Присвоить значение переменной хА – координата точки А по оси х.
3. Присвоить значение переменной уА – координата точки А по оси у.
4. Присвоить значение переменной RА: = sqrt(xA^2 +yA^2). Это расстояние точки А до начала координат.
5. Определить координаты точки В.
6. Присвоить значение переменной хВ – координата точки В по оси х.
7. Присвоить значение переменной уВ – координата точки В по оси у.
8. Присвоить значение переменной RВ: = sqrt(xВ^2 +yВ^2). Это расстояние точки В до начала координат.
9. Если RА< RВ , вывести ответ «Точка А ближе к началу координат». Иначе выполнить условие:
10. Если RА> RВ, вывести ответ «Точка В ближе к началу координат». Иначе вывести ответ «Точки А и В равноудалены от начала координат».
нц пока день недели НЕ «воскресенье»
встать пораньше, собраться, идти в школу
кц
б) из литературного произведения:
Он затаился в темноте. Мими украдкой переглядывалась с ним. Она стояла на противоположной стороне улицы. Салим смотрел на нее и ждал, пока она одернет юбку, — такой условный сигнал они установили. Она стояла чуть в стороне от остальных девушек, не обращая внимания на машины, которые останавливались рядом. Сегодня ей предстояло другое.
затаиться в темноте
нц
перегянуться и наблюдать
кц при она одернет юбку
в) из любой предметной области, изучаемой в школе:
1) Запас А:= А + 0.15*А – В
2) Прибавить год N:=N+1
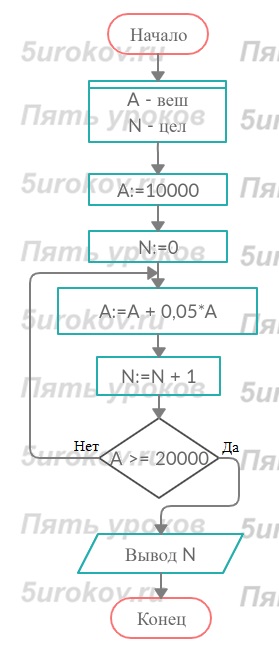
Используем Цикл с заданным условием окончания работы (цикл-ДО, цикл с постусловием).
До А < С все будет работать. Потом план выполняться уже не будет, т.к. запас рыб не восполнится.
Число будет А - натуральное. Для подсчета количества операций вводим N – тоже натуральное число.
Ответ: n=32, m=5.
б) После выполнения следующего алгоритма Чертёжник вернулся в исходную точку. Какие числа надо записать вместо a и b?
x * y = x + x + … + x.
Начальное значение z = 0. Когда мы добавляем слагаемое в сумму, количество слагаемых, которое нужно еще добавить, уменьшается на 1. Суммирование продолжается, пока количество слагаемых больше нуля.
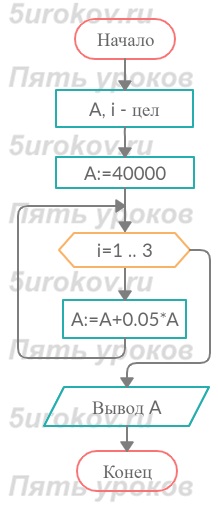
Переменная А - численность населения.
Я думаю, что могут. К примеру можно записать короткий алгоритм с циклом, но действий повторяться может много.
б) Краткость алгоритма и скорость его выполнения совпадают?
Также и тут, если алгоритм короткий но с циклом, который может повториться множество раз, он может уступить по скорость длинному алгоритму но с линейной последовательностью. Решение заданий из учебника Информатика 8 класс Босова, параграф 2.4 Основные алгоритмические функции. Следование, ветвление, повторение.
Задание 1. Ознакомьтесь с материалами презентации к параграфу, содержащейся в электронном приложении к учебнику. Используйте эти материалы при подготовке ответов на вопросы и выполнении заданий.
Презентации: Основные алгоритмические конструкции. Следование – Скачать презентациюОсновные алгоритмические конструкции. Ветвление – Скачать презентацию
Основные алгоритмические конструкции. Повторение – Скачать презентацию
Задание 2. Какие алгоритмы называются линейными? Зависит ли в линейном алгоритме последовательность выполняемых действий от исходных данных?
Линейные алгоритмы – алгоритмы, в которых используется алгоритмическая конструкция «Следование», отображающая естественный, последовательный порядок действий.В линейном алгоритме не зависит последовательность выполняемых действий от исходных данных, так как алгоритм выполняет последовательный порядок действий без повторов.
Задание 3. Приведите пример линейного алгоритма.
а) из повседневной жизни:Алгоритм как собраться в школу
1. Поставить будильник на 7 00 утра
2. Проснуться в 7 00
3. Выключить будильник
4. Пойти умываться
5. Позавтракать
6. Собрать учебники , тетради, пенал
7. Одеться
8. Взять вторую обувь
9. Выйти из дома.
б) из литературного произведения:
Алгоритм как разбудить ребенка из стихотворения
1. Лучик солнечный проснулся,
2. Улыбнулся,
3. потянулся
4. И пошёл будить сестричек —
Маленьких весёлых птичек.
5. Птички песенку запели,
6. И проснулся лес от трели.
7. Нежно глазки открывая,
Встала феечка лесная,
8. Разбудила медвежат,
И зайчаток, и мышат,
9. Полетела помогать
Всех девчонок поднимать.
10. Сядет фея на подушку,
11. «С добрым утром!» — шепнёт в ушко,
12. Поцелует нос и щёчки
Маминой любимой дочке,
13. Тихо скажет: «Динь-дилень!
Пусть хорошим будет день!»
в) из любой предметной области, изучаемой в школе:
Построение таблиц истинности для логических выражений
1. подсчитать n — число переменных в выражении;
2. подсчитать общее число логических операций в выражении;
3. установить последовательность выполнения логических операций с учётом скобок и приоритетов;
4. определить число столбцов в таблице: число переменных + число операций;
5. заполнить шапку таблицы, включив в неё переменные и операции в соответствии с последовательностью, установленной в п.3;
6. определить число строк в таблице (не считая шапки таблицы): m=2n;
7. выписать наборы входных переменных с учётом того, что они представляют собой целый ряд n-разрядных двоичных чисел от 0 до 2n - 1;
8. провести заполнение таблицы по столбцам, выполняя логические операции в соответствии с установленной последовательностью.
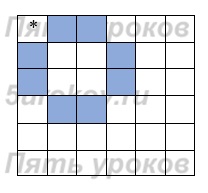
Задание 4. Запишите линейный алгоритм, исполняя который Робот нарисует на клетчатом поле следующий узор и вернётся в исходное положение.

алг Узор нач Вправо Закрасить Вправо Закрасить Вправо Вниз Закрасить Вниз Закрасить Вниз Влево Закрасить Влево Закрасить Влево Вверх Закрасить Вверх Закрасить Вверх кон
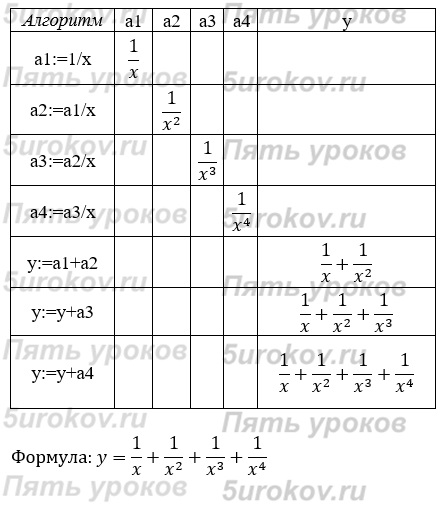
Задание 5. По алгоритму восстановите формулу.
a1 :=1/x
а2:=a1/x
а3:=а2/х
а4:=а3/х
y:=a1+a2
у:=у+а3
у:=у+а4

Задание 6. Какое значение получит переменная у после выполнения алгоритма?
| х:=1 | х:=1 | x |
|---|---|---|
| у:=2*х | 2*1=2 | 2 |
| у:=у+3 | 2+3=5 | 2x+3 |
| у:=у*х | 5*1=5 | (2х+3)х |
| у:=у+4 | 5+4=9 | (2х+3)х+4 |
| у:=у*х | 9*1=9 | ((2х+3)х+4)х |
| у:=у+5 | 9+5=14 | ((2х+3)х+4)х+5 |
Ответ: у = ((2х + 3)х + 4)х + 5; у = 14 при х= 1.
Задание 7. Для заданного количества суток (tfh) требуется определить количество часов (h), минут (т) и секунд (с).
| Алгоритм | tfh | 1 | 2 | 1/2 |
|---|---|---|---|---|
| h:=tfh*24 | h | 24 | 48 | 12 |
| m:=h*60 | m | 1440 | 2880 | 720 |
| c:=m*60 | c | 86400 | 172800 | 43200 |
Задание 8. Известно, что 1 миля =7 вёрст, 1 верста = 500 саженей, 1 сажень – 3 аршина, 1 аршин = 28 дюймов, 1 дюйм = 25,4 мм. Пользуясь этой информацией, составьте линейный алгоритм перевода расстояния X миль в километры.
K – коэффициент для перевода из миль в км; 1 миля = 7 вёрст, 1 верста = 500 саженей, 1 сажень = 3 аршина, 1 аршин = 28 дюймов, 1 дюйм = 25,4 мм, 1 км = 106 мм 1м = 1000 мм и 1 км = 1000 м, поэтому 106алг Перевод расстояния Х миль в км арг К, х, у - вещественное число рез у нач К := 7 * 500 * 3 * 28 * 25,4 / 106 у: = К * х кон
Задание 9. Исходное данное — целое трёхзначное число х. Выполните для х = 125 следующий алгоритм.
a:=x div 100
b:=x mod 100 div 10
c:=x mod 10
s :=a+b+c
Какой смысл имеет результат s этого алгоритма?

Смысл результата – это сумма цифр числа х
Задание 10. Определите значение целочисленных переменных х и у после выполнения алгоритма.
х:=336
У:=8
х:=х div у
у:=х mod у

Задание 11. Какие алгоритмы называют разветвляющимися? Согласны ли вы с утверждением, что в разветвляющемся алгоритме при любых исходных данных выполняются все действия, предусмотренные алгоритмом?
Алгоритмы, в основе которых лежит структура «ветвление», называют разветвляющимися.Нет не согласен, при разветвляющимися алгоритме, в зависимости от результатов проверки условия, выполняется одна из двух последовательностей действий.
Задание 12. Приведите пример разветвляющегося алгоритма.
а) из повседневной жизни:Подготовка домашнего задания
1. Определить список уроков на завтра по расписанию.
2. Если завтра есть математика или физика, то позаниматься с репетитором.
Если нет, перейти к п.4.
4. Определить, что задали по каждому уроку из расписания на завтра.
5. Выполнить домашнее задание по каждому уроку.
Или вот такой:
Погреть себе еды
1. Взять тарелку.
2. Если тарелка гразная, помыть ее.
3. Положить еду.
4. Поставить в микроволновку.
б) из литературного произведения:
Как обвенчаться
Ромео и Джульета влюбляются друг в друга.
Если их семьи враждуют, венчаться тайно. В противном случае играть пышную свадьбу.
в) из любой предметной области, изучаемой в школе.
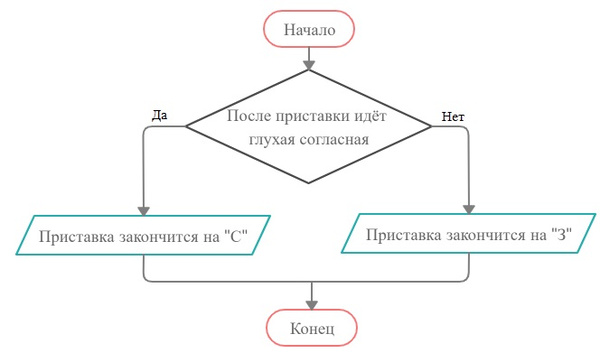
алг правописание частиц НЕ, НИ нач если частица под ударением то писать НЕ иначе писать НИ все кон
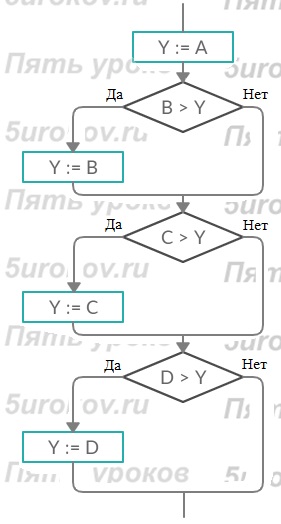
Задание 13. Дополните алгоритм из примера 9 так, чтобы с его помощью можно было найти наибольшую из четырёх величин А, В, С и D.

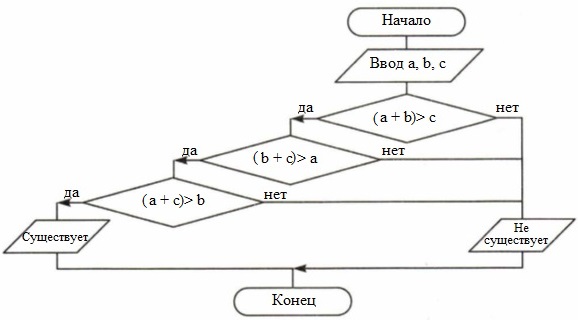
Задание 14. Составьте алгоритм, с помощью которого можно определить, существует ли треугольник с длинами сторон а, b, с.
Треугольник не будет существовать, если сумма длин 2 любых сторон будет меньше и равна длине третьей стороны.
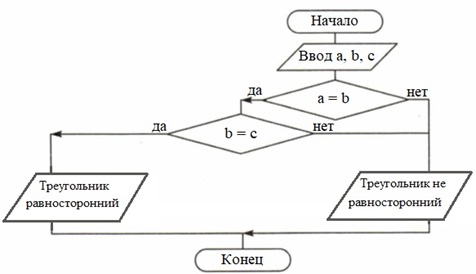
Задание 15. Составьте алгоритм, с помощью которого можно определить, является ли треугольник с заданными длинами сторон а, b, с равносторонним.

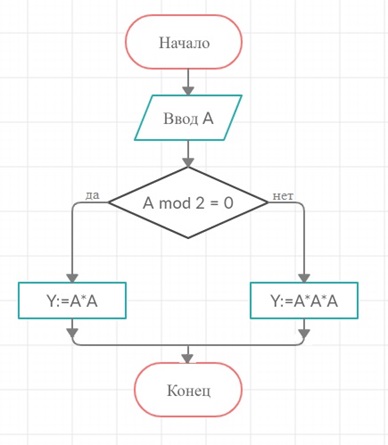
Задание 16. Составьте алгоритм возведения чётного числа в квадрат, а нечётного – в куб.

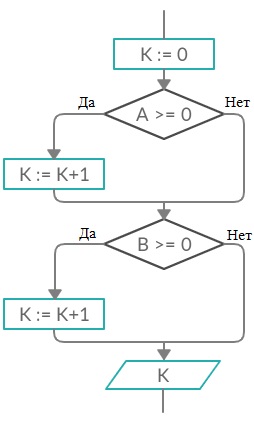
Задание 17. Какая задача решается с помощью следующего алгоритма?

Ответ: Данный алгоритм считает количество неотрицательных чисел среди двух чисел A и B.
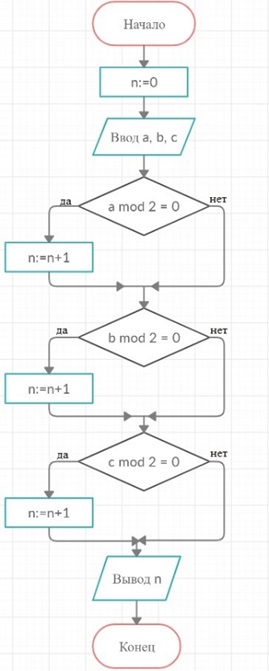
Задание 18. Составьте блок-схему алгоритма определения количества чётных чисел среди заданных целых чисел А, B и С.

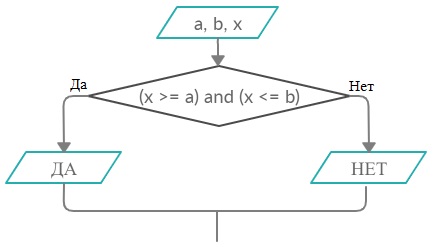
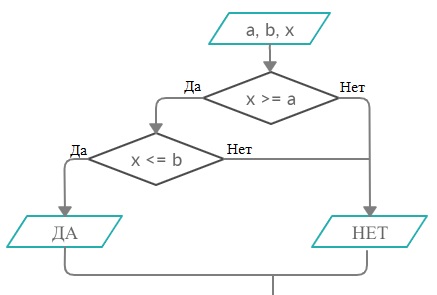
Задание 19. Составьте блок-схему алгоритма определения принадлежности точки x отрезку [a, b] (пример 8) с использованием комбинации из двух ветвлений.
Пример 8 из учебника:
Решение:

Задание 20. Составьте блок-схему алгоритма правописания приставок, оканчивающихся на букву «з».

Задание 21. Известно, что 31 января 2011 года было понедельником. Какие значения должны быть присвоены литерной переменной у в алгоритме, определяющем день недели для произвольного числа (chislo) января 2011 года?
chislo:=chislo mod 7если chislo=3 то y:=’Понедельник’
если chislo=4 то y:=’Вторник’
если chislo=5 то y:=’Среда’
если chislo=6 то y:=’Четверг’
если chislo=0 то y:=’Пятница’
если chislo=1 то y:=’Суббота’
если chislo=2 то y:=’Воскресенье’
Сначала найдём понедельник 31-го января по формуле: chislo:=chislo mod 7, где chislo = 31.
31 mod 7 = 31/7 (ост) = 31 – 4*7 = 31-28 = 3
То есть, для chislo = 3 будет y='Понедельник'
Найдём для остальных дней января:
30 mod 7 = 2 – то есть будет воскресенье для chislo=2, так как предыдущий день. И так далее.
Задание 22. Даны две точки на плоскости. Определите, какая из них находится ближе к началу координат.
Посмотрите задание 145 из рабочей тетради.Нам нужно посчитать сначала 2 расстояния по координатам, и потом их сравнить. Ответом будет минимальное.
Алгоритм:
1. Определить координаты точки А.
2. Присвоить значение переменной хА – координата точки А по оси х.
3. Присвоить значение переменной уА – координата точки А по оси у.
4. Присвоить значение переменной RА: = sqrt(xA^2 +yA^2). Это расстояние точки А до начала координат.
5. Определить координаты точки В.
6. Присвоить значение переменной хВ – координата точки В по оси х.
7. Присвоить значение переменной уВ – координата точки В по оси у.
8. Присвоить значение переменной RВ: = sqrt(xВ^2 +yВ^2). Это расстояние точки В до начала координат.
9. Если RА< RВ , вывести ответ «Точка А ближе к началу координат». Иначе выполнить условие:
10. Если RА> RВ, вывести ответ «Точка В ближе к началу координат». Иначе вывести ответ «Точки А и В равноудалены от начала координат».
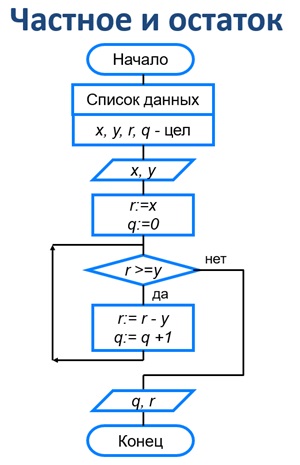
Задание 23. Определите, есть ли среди цифр заданного целого трёхзначного числа одинаковые.
Задание 146 в рабочей тетради. Для это вспоминаем задачку, которая раскладывала трехзначное число на цифры a, b, c и потом их складывала в S. Используем оттуда готовые формулы, чтобы присвоить нашим переменным a, b, c соответствующие значения. А потом останется только сравнить a, b, c между собой. Это была задача 129 в раб.тетради и зад. 9 в данном учебнике. Оттуда берем первые шаги по присвоению a, b, c.алг Определение наличия одинаковых цифр в трехзначном числе арг цел x, a, b, c, лит R рез R нач ввести Х a:=x div 100 b:=x mod 100 div 10 c:=x mod 10 если (a=b) and (a=c) and (b=c) то R:= «В данном числе есть одинаковые цифры» иначе R:= «В данном числе все цифры разные» все вывести R кон
Задание 24. Приведите пример циклического алгоритма:
а) из повседневной жизни:нц пока день недели НЕ «воскресенье»
встать пораньше, собраться, идти в школу
кц
б) из литературного произведения:
Он затаился в темноте. Мими украдкой переглядывалась с ним. Она стояла на противоположной стороне улицы. Салим смотрел на нее и ждал, пока она одернет юбку, — такой условный сигнал они установили. Она стояла чуть в стороне от остальных девушек, не обращая внимания на машины, которые останавливались рядом. Сегодня ей предстояло другое.
затаиться в темноте
нц
перегянуться и наблюдать
кц при она одернет юбку
в) из любой предметной области, изучаемой в школе:

Задание 25. Напишите алгоритм, под управлением которого Робот обойдёт прямоугольную область, обнесённую стеной, по периметру и закрасит угловые клетки. Размеры области неизвестны.

нач закрась нц пока справа свободно вправо кц закрась нц пока снизу свободно вниз кц закрась нц пока слева свободно влево кц закрась кон
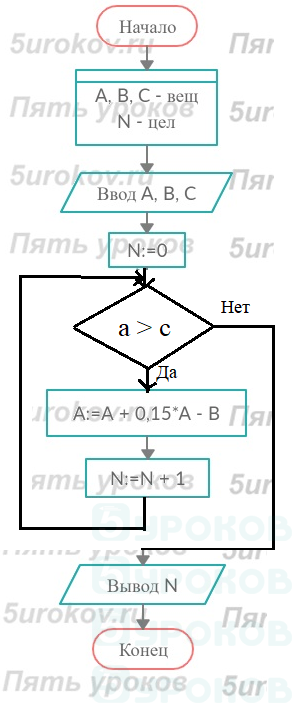
Задание 26. Запас рыбы в пруду оценён в А тонн. Ежегодный прирост рыбы составляет 15%. Ежегодный план отлова – В тонн. Наименьший запас рыбы составляет С тонн. (Запас ниже С тонн уже не восстанавливается.) Составьте блок-схему алгоритма для подсчёта количества лет, в течение которых можно выдерживать заданный план.
В цикле будет:1) Запас А:= А + 0.15*А – В
2) Прибавить год N:=N+1
Используем Цикл с заданным условием окончания работы (цикл-ДО, цикл с постусловием).
До А < С все будет работать. Потом план выполняться уже не будет, т.к. запас рыб не восполнится.

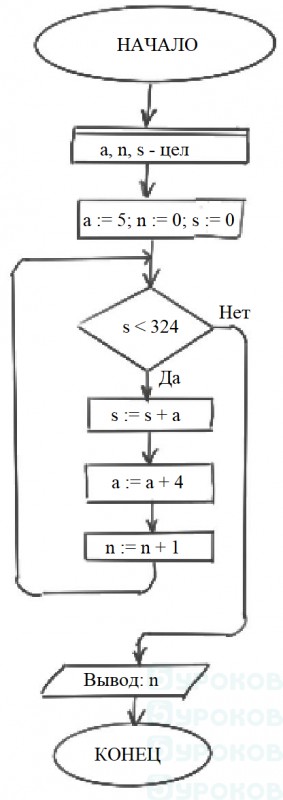
Задание 27. Дана последовательность 5, 9, 13, 17, ... . Составьте блок-схему алгоритма для определения числа слагаемых, сумма которых равна 324.

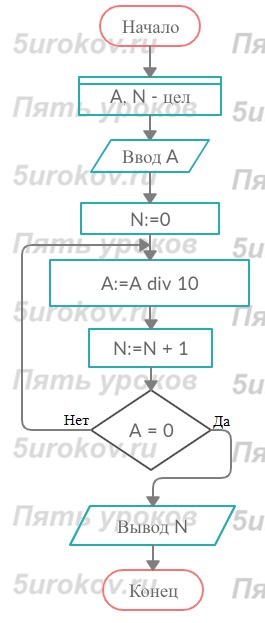
Задание 28. Составьте алгоритм для определения количества цифр в записи произвольного натурального числа.
Используем функцию DIV 10 , чтобы каждый раз сокращать на 1 разряд до тех пор, пока результат такого деления не приведет к 0, т.е. , например, 5 div 10 получаем 0 целых.Число будет А - натуральное. Для подсчета количества операций вводим N – тоже натуральное число.

Задание 29. Сумма 10 000 рублей положена в сберегательный банк, при этом прирост составляет 5% годовых. Составьте алгоритм, определяющий, через какой промежуток времени первоначальная сумма увеличится в два раза.

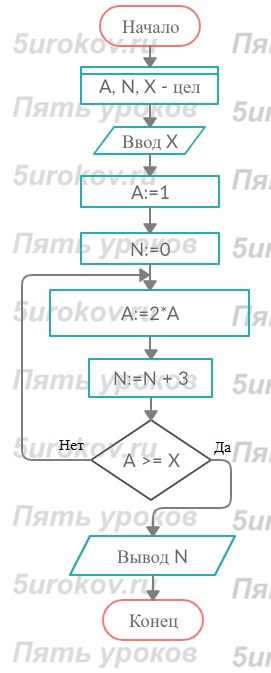
Задание 30. Одноклеточная амёба каждые три часа делится на 2 клетки. Составьте алгоритм вычисления времени, через которое будет X амёб.

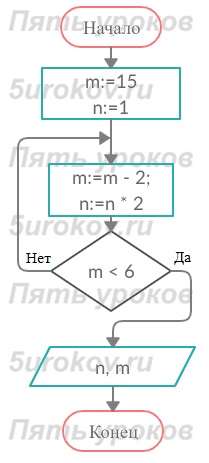
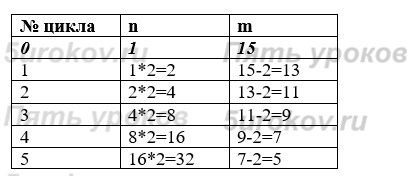
Задание 31. Определите значения переменных n, m после выполнения алгоритма.


Ответ: n=32, m=5.
Задание 32. Исполнитель Чертежник находится в произвольной точке координатной плоскости.
а) Выясните, где окажется Чертежник после выполнения следующего алгоритма:алг нач нц 6 раз сместиться на вектор (4, 6) сместиться на вектор (-2, -4) кц сместиться на вектор (-12, -12) конОтвет: Чертежник окажется на исходной точке.
б) После выполнения следующего алгоритма Чертёжник вернулся в исходную точку. Какие числа надо записать вместо a и b?
алг нач нц 7 раз сместиться на вектор (0, 2) сместиться на вектор (a, 0) сместиться на вектор (0, b) сместиться на вектор (-1, 0) кц сместиться на вектор (-7, -7) конОтвет: a = 2, b = -1.
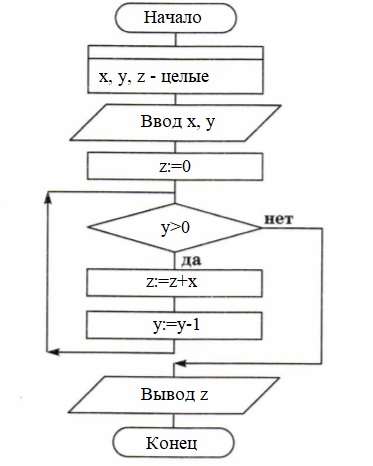
Задание 33. Составьте алгоритм нахождения произведения z двух натуральных чисел х и у без использования операции умножения.
Произведение чисел x и y можно получить в виде суммы, состоящая из y слагаемых, каждое из которых равно x:x * y = x + x + … + x.
Начальное значение z = 0. Когда мы добавляем слагаемое в сумму, количество слагаемых, которое нужно еще добавить, уменьшается на 1. Суммирование продолжается, пока количество слагаемых больше нуля.

Задание 34. Население города Н увеличивается на 5% ежегодно. В текущем году оно составляет 40 000 человек. Составьте блок-схему алгоритма вычисления предполагаемой численности населения города через 3 года. Составьте таблицу значений переменных, задействованных в алгоритме.
Используем цикл с заданным числом повторений (цикл – ДЛЯ, цикл с параметром).Переменная А - численность населения.

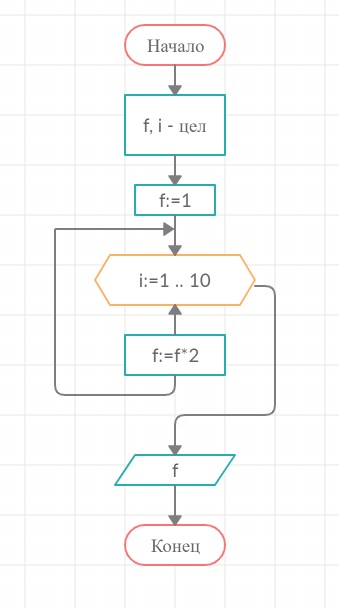
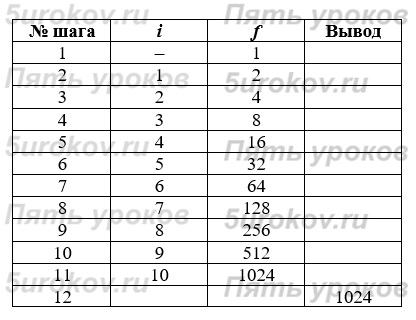
Задание 35. Каждая бактерия делится на две в течение 1 минуты. В начальный момент имеется одна бактерия. Составьте блок-схему алгоритма вычисления количества бактерий через 10 минут. Исполните алгоритм, фиксируя каждый его шаг в таблице значений переменных.


Задание 36. Согласные ли вы со следующими утверждениями:
а) Короткие алгоритмы могуть описывать длинные последовательности действий.Я думаю, что могут. К примеру можно записать короткий алгоритм с циклом, но действий повторяться может много.
б) Краткость алгоритма и скорость его выполнения совпадают?
Также и тут, если алгоритм короткий но с циклом, который может повториться множество раз, он может уступить по скорость длинному алгоритму но с линейной последовательностью. Решение заданий из учебника Информатика 8 класс Босова, параграф 2.4 Основные алгоритмические функции. Следование, ветвление, повторение.
