Ответы по параграфу 2.3 Объекты алгоритмов
Величины делятся на:
Постоянные – значения указываются в тексте алгоритма и не меняются в процессе его исполнения.
Переменные – значения меняются в процессе исполнения алгоритма.
• Числовой: целая, вещественная;
• Текстовый: символьная (один символ), литеральная (строка символов);
• Логический: да (истина, true, 1), нет (ложь, false, 0).
2) Недопустимое по типу
3) Недопустимое по значению
Записывается так: <имя переменной> := <выражение>
Основные свойства:
• Пока переменной не присвоено значение, она остаётся неопределённой.
• Значение, присвоенное переменной, сохраняется до следующего присваивания.
• Если переменной присваивается новое значение, то предыдущее её значение теряется.
б) А=В – неверно, не хватает двоеточия(:) после знака равно(=);
в) А=В+1 – неверно, не хватает двоеточия(:) после знака равно(=);
г) А+1:=А – неверно, т.к. слева не должно быть арифметики – только название самой переменной.
Если А и В — числовые величины, то обмен их значениями можно организовать и без промежуточной переменной, например так:
А:=А+В В:=А-В А:=А-В
Тогда алгоритм будет выглядеть вот так:
a->b, b->c, c->a. Как задача про сосуды в учебнике, только теперь их не 2, а 3. Нужно ввести промежуточную переменную - m. Алгоритм будет следующий:
X=X1=3
Y=Y0=5
X0=X1-Y0 = 3-5=-2
Ответ: х=-2, у=5
Выражения состоят из операндов (констант, переменных, функций), объединённых знаками операций. Основные правила записи выражений:
Выражения записываются в виде линейных последовательностей символов (без подстрочных и надстрочных символов, обыкновенных дробей и т. д.); знаки операций пропускать нельзя. Порядок выполнения операций определяется скобками и приоритетом (старшинством) операций; операции одинакового приоритета выполняются слева направо.
Различают арифметические, логические и строковые выражения.
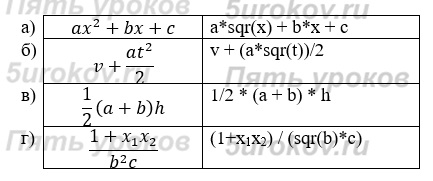
Задание 15. Запишите логическое выражение, истинное при выполнении указанного условия и ложное в противном случае:
а) (x >= 0) И (x <= 1)
б) (x < 0) ИЛИ (x > 1)
в) (x > 0) И (y > 0)
г) (х > 0) ИЛИ (у > 0)
д) (x <= 0) И (у <= 0)
е) ((х > 0) И (у <= 0)) ИЛИ ((у > 0) И (х <= 0))
б) (у >= х) и (у >= -х) и (у <= 1)
1) Смотрим линию y=x+4
Если х=4, то у должен быть 4 и меньше, чтобы попасть в серую зону
Значит, у <= x+4
2) Смотрим линию y=x-4
Если х=4, то у должен быть -4 и больше, чтобы попасть в серую зону
Значит, у >= x-4
3) Объединяем 2 условия в логическое выражение:
(у <= x+4) И (у >= x-4)
Ответ: (у<= x+4) И (у >= x-4)
Задание 18. Запишите команду присваивания, в результате выполнения которой логическая переменная t получает значение TRUE, если выполняется указанное условие, и значение FALSE в противном случае:
Аналог задания 125 в рабочей тетради.
a) t:=x>0;
б) t:= (х=0) или (y=0) или (z=0)
в) t:= (x=z) и (y=z) – третье равенство писать не нужно, т.к оно следует и первых двух
Решение заданий из учебника Информатика 8 класс Босова, параграф 2.3 Объекты алгоритмов. Величины, выражения, команда присваивания, табличные величины.
Задание 1. Ознакомьтесь с материалами презентации к параграфу, содержащейся в электронном приложении к учебнику. Что вы можете сказать о формах представления информации в презентации и в учебнике? Какими слайдами вы могли бы дополнить презентацию?
Скачать презентациюЗадание 2. Что такое величина? Чем отличаются постоянные и переменные величины?
Величина в информатике – это отдельный информационный объект (число, символ, строка, таблица и др.).Величины делятся на:
Постоянные – значения указываются в тексте алгоритма и не меняются в процессе его исполнения.
Переменные – значения меняются в процессе исполнения алгоритма.
Задание 3. Величины каких типов используются при записи алгоритмов?
Типы величин в алгоритме:• Числовой: целая, вещественная;
• Текстовый: символьная (один символ), литеральная (строка символов);
• Логический: да (истина, true, 1), нет (ложь, false, 0).
Задание 4. Укажите тип величины, если её значение равно.
| Значение | Тип величины |
|---|---|
| 2020 | Целое |
| 14.48 | Вещественное |
| 'ДА' | Литерная |
| FALSE | Логический |
| -125 | Целое |
| '142' | Литерная |
| 1,4 * 105 | Целое, могло быть записано как 1,4Е+5 |
| .123Е-2 | 0,123*10-2=0,00123 - вещественное |
| 'пять' | Литерная |
Задание 5. Определите типы следующих величин.
| Величина | Тип величины |
|---|---|
| Вес человека | Вещественное (65.77) |
| Марка автомобиля | Литерная (AUDI) |
| Год вашего рождения | Целое (2006) |
| Площадь фигуры | Вещественное (45,5) |
| Название месяца года | Литерная (Февраль) |
| Количество мест в самолете | Целое (526) |
Задание 6. Приведите по одному примеру допустимых и недопустимых значений для каждой из величин.
1) Допустимое2) Недопустимое по типу
3) Недопустимое по значению
| Температура человека | 1) 36.5 2) Хорошая 3) 100о С |
| Скорость автомашины | 1) 60 км/ч 2) Высокая 3) 10000 км/ч |
| Площадь страны | 1) 50 км2 2) Большая 3) 1 см2 |
| Название дня недели | 1) Понедельник 2) 1232214 3) Праздник |
Задание 7. Для чего предназначена команда присваивания? Каковы её основные свойства?
Она предназначена задать конкретное значение величины.Записывается так: <имя переменной> := <выражение>
Основные свойства:
• Пока переменной не присвоено значение, она остаётся неопределённой.
• Значение, присвоенное переменной, сохраняется до следующего присваивания.
• Если переменной присваивается новое значение, то предыдущее её значение теряется.
Задание 8. Какие команды присваивания составлены правильно?
а) А:=В – верно;б) А=В – неверно, не хватает двоеточия(:) после знака равно(=);
в) А=В+1 – неверно, не хватает двоеточия(:) после знака равно(=);
г) А+1:=А – неверно, т.к. слева не должно быть арифметики – только название самой переменной.
Задание 9. Придумайте свой алгоритм обмена значениями числовых переменных А и В.
Такой алгоритм подходит для любых переменных, даже литерных:алг обмен значениями (лит А, В) арг А, В рез А, В нач лит М М:=А А:=В В:=М кон
Если А и В — числовые величины, то обмен их значениями можно организовать и без промежуточной переменной, например так:
А:=А+В В:=А-В А:=А-В
Тогда алгоритм будет выглядеть вот так:
алг обмен значениями (вещ А, В) арг А, В рез А, В нач А:=А+В В:=А-В А:=А-В кон
Задание 10. Сколько промежуточных переменных потребуется для того, чтобы переменной А было присвоено значение переменной В, переменной В — значение переменной С, а переменной С — значение переменной А? Запишите соответствующий алгоритм на алгоритмическом языке.
Ответ: Не более одной переменной.a->b, b->c, c->a. Как задача про сосуды в учебнике, только теперь их не 2, а 3. Нужно ввести промежуточную переменную - m. Алгоритм будет следующий:
алг обмен значениями (лит а, b, c) арг a, b, c рез a, b, c нач лит m m:=a a:=b b:=c c:=m кон
Задание 11. После выполнения команды присваивания х:=х+у значение переменной х равно 3, а значение переменной у равно 5. Чему были равны значения переменных х и у до выполнения указанной команды присваивания?
Х1=Х0 + Y0 => X0=X1-Y0X=X1=3
Y=Y0=5
X0=X1-Y0 = 3-5=-2
Ответ: х=-2, у=5
Задание 12. Что называют выражением? Каковы основные правила записи выражений?
Выражение – языковая конструкция для вычисления значения с помощью одного или нескольких операндов.Выражения состоят из операндов (констант, переменных, функций), объединённых знаками операций. Основные правила записи выражений:
Выражения записываются в виде линейных последовательностей символов (без подстрочных и надстрочных символов, обыкновенных дробей и т. д.); знаки операций пропускать нельзя. Порядок выполнения операций определяется скобками и приоритетом (старшинством) операций; операции одинакового приоритета выполняются слева направо.
Различают арифметические, логические и строковые выражения.
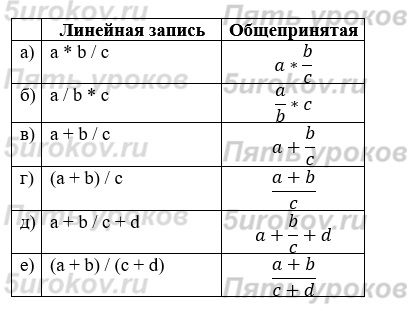
Задание 13. Переведите из линейной записи в общепринятую.

Задание 14. Запишите на школьном алгоритмическом языке.
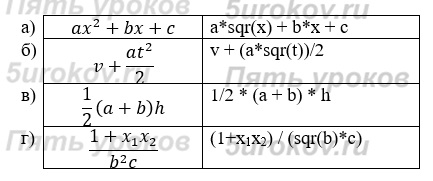
Задание 15. Запишите логическое выражение, истинное при выполнении указанного условия и ложное в противном случае:
а) х принадлежит отрезку [0, 1];
б) х лежит вне отрезка [0, 1];
в) каждое из чисел х, у положительно;
г) хотя бы одно из чисел х, у положительно;
д) ни одно из чисел х, у не является положительным;
е) только одно из чисел х, у положительно.
а) (x >= 0) И (x <= 1)б) (x < 0) ИЛИ (x > 1)
в) (x > 0) И (y > 0)
г) (х > 0) ИЛИ (у > 0)
д) (x <= 0) И (у <= 0)
е) ((х > 0) И (у <= 0)) ИЛИ ((у > 0) И (х <= 0))
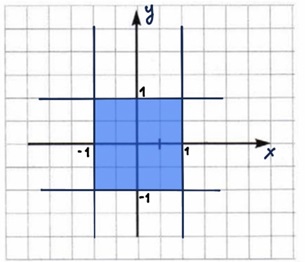
Задание 16. Изобразите в декартовой прямоугольной системе координат область, в которой и только в которой истинны следующие логические выражения:
а) (х >= -1) И (х <= 1) И (у >= -1) И (у <= 1);
б) (у >= х) и (у >= -х) и (у <= 1)

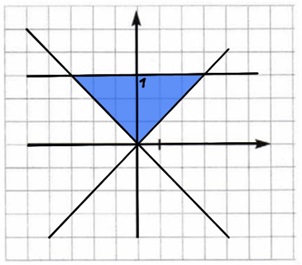
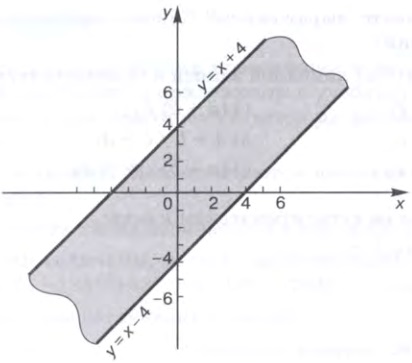
Задание 17. Запишите логическое выражение, принимающее значение TRUE, когда точка с координатами (х, у) принадлежит закрашенной области.

1) Смотрим линию y=x+4
Если х=4, то у должен быть 4 и меньше, чтобы попасть в серую зону
Значит, у <= x+4
2) Смотрим линию y=x-4
Если х=4, то у должен быть -4 и больше, чтобы попасть в серую зону
Значит, у >= x-4
3) Объединяем 2 условия в логическое выражение:
(у <= x+4) И (у >= x-4)
Ответ: (у<= x+4) И (у >= x-4)
Задание 18. Запишите команду присваивания, в результате выполнения которой логическая переменная t получает значение TRUE, если выполняется указанное условие, и значение FALSE в противном случае:
а) х – положительное число;
б) хотя бы одно из чисел х, у, z равно нулю;
в) числа х, у, z равны между собой.
Аналог задания 125 в рабочей тетради.a) t:=x>0;
б) t:= (х=0) или (y=0) или (z=0)
в) t:= (x=z) и (y=z) – третье равенство писать не нужно, т.к оно следует и первых двух
Задание 19. Какие из приведённых ниже величин целесообразно представлять с помощью таблиц?
| Величины | Представление |
|---|---|
| Список учеников класса | Линейная таблица (одномерный массив) |
| Рост учеников класса | Прямоугольная таблица (двумерный массив) |
| Средний рост учеников класса | Если 1 цифра, не нужна таблица |
| Оценка ученика по физике | Если фамилия, физика и оценка, то Прямоугольная таблица; Если это Фамилия и оценка, то уже таблица линейная; Если это просто 1 цифра в контексте, то не нужна таблица. |
| Средний балл ученика по физике | Аналогично примеру выше |
| Оценки учеников за контрольную работу по информатике | Прямоугольная таблица (двумерный массив) |
| Длины сторон треугольника | Можно представить как Линейная таблица (одномерный массив) |
| Длины сторон нескольких треугольников | Можно представить как Прямоугольная таблица (двумерный массив) |
| Названия дней недели | Можно представить как Линейная таблица (одномерный массив) |
| Имя человека | Это одно значение, нет смысла в таблице |
| Площадь фигуры | Это одно значение, нет смысла в таблице |
| Периметры нескольких прямоугольников | Можно представить как Прямоугольная таблица (двумерный массив) |
| Самая холодная температура воздуха в январе | Это одно значение, нет смысла в таблице; Но если мы хотим видеть статистику по январю, чтобы там увидеть минимальное значение, то такая статистика будет в таблицу. Либо как с физикой мы говорим о 2 показателях – температура и январь – тогда таблица. |
| Количество девочек в классе | Это одно значение, нет смысла в таблице. |
| Самая дождливая декада июня | Аналогично температуре в январе. Если просто декада – то это чисто информация для 1 ячейки (величина), если мы учитываем еще и июнь, то это уже линейная таблица, если же мы сравниваем еще и с другими декадами в статистике – то прямоугольная таблица. |
