---

---

Задание 23. В трёх седьмых классах 70 ребят. Из них 27 занимаются в драмкружке, 32 поют в хоре, 22 увлекаются спортом. В драмкружке — 10 ребят из хора, в хоре — 6 спортсменов, в драмкружке — 8 спортсменов; 3 спортсмена посещают и драмкружок, и хор.
Сколько ребят не поют в хоре, не увлекаются спортом и не занимаются в драмкружке?
Сколько ребят занято только спортом?


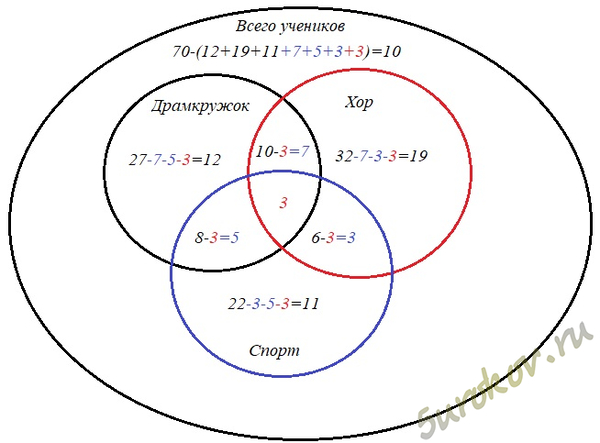
1) Наше условие "3 спортсмена посещают и драм кружок и хор" соответствует красной цифре 3 на картинке.
2) 10 учеников посещают и драмкружок и хор. В пересечении Драмкружка и Хора должна стоять число 10, но у нас еще идёт пересечение с областью(цифра 3). Из 10-ти вычитаем 3 и получим число 7. Таким образом 7-ро учеников ходят в драмкружок и хор, но не увлечены спортом.
3) Аналогично действию (2) делаем с высказыванием, что в хоре 6 спортсменов. Тут нам нужно найти разность 6-3=3.
4) В драмкружке 8 спортсменов. Значит 5-ро занимаются спортом и посещают драмкружок, но не интересуются хором.
5) Чтобы найти количество учеников, которым интересно только одно направление, например хором, найдём разность общего количества ребят в хоре и пересекающие нам области(7+3+3), то есть 32-(7+3+3)=19. Действуя аналогично с другими интересами ребят получаем, что только драмкружком интересуются 12 ребят, а только спортом 11.
6) Найдем учеников, которые ничем не заняты. Для этого вычтем из общего числа учеников(70), учеников кто хоть чем-то занят(60). Получаем 10 ребят ничем не интересуются.
Ответ: 10 человек не поют в хоре, не увлекаются спортом и не занимаются в драмкружке; 11 ребят заняты только спортом.

Сообщить об ошибке Добавить своё решение

Запиши свой ответ здесь (кратко и понятно)

Отправить ответ

Сообщение об ошибке

Суть проблемы:

Подтвердите, что вы не робот:

Закрыть Отправить сообщение